UFC 3-440-01
14 June 2002
weather variables I and Ta. The type of process load and system configuration determines
the relative circulation fluid temperature, Ti.
(d) Collector Efficiency Plot. Equation F-1 can be rewritten as a
dimensionless "efficiency" equation by dividing both sides by the product of I and Ac:
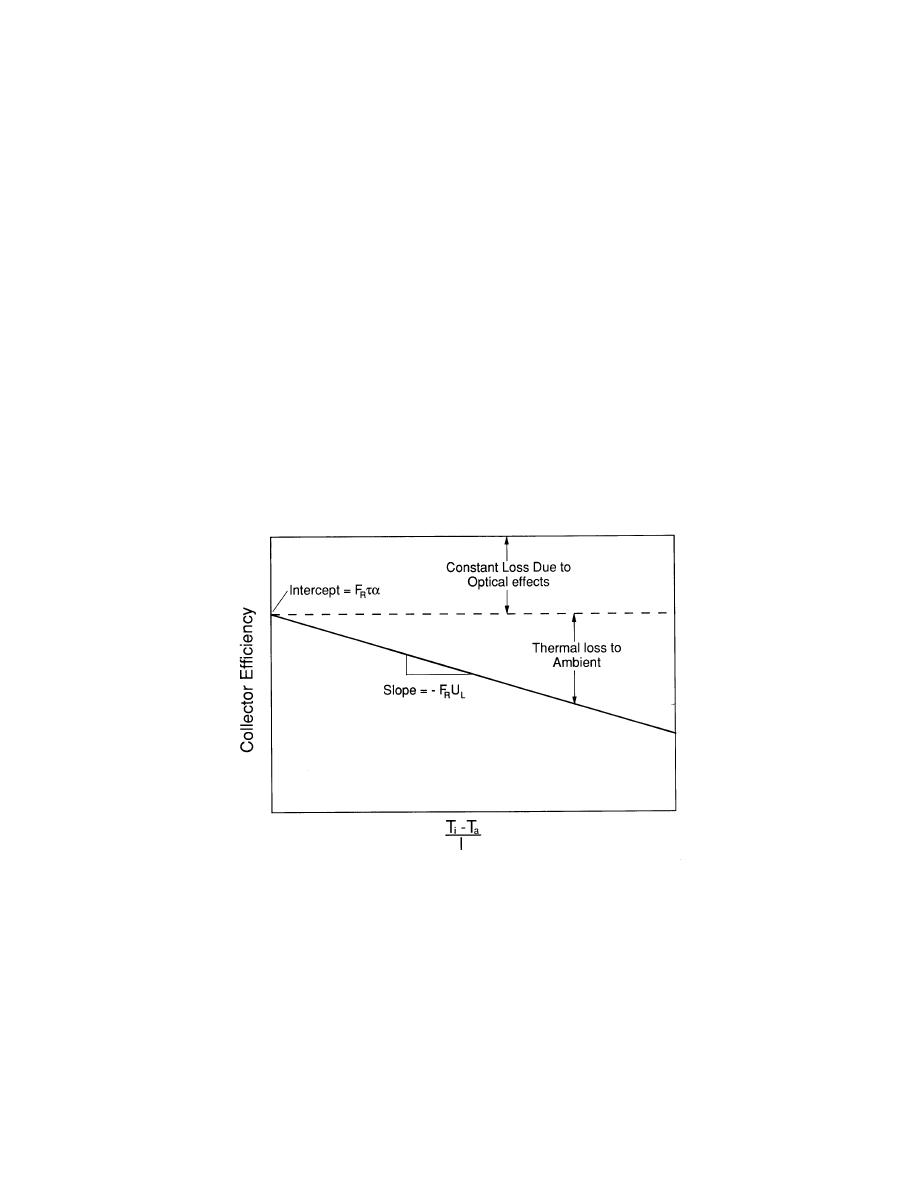
Collector Efficiency = FRta - FRUL(Ti - Ta) / I
(eq. F-2)
Note that this efficiency equation is dependent on only one variable that is a combination of
I, Ti, and Ta. This allows it to be graphed in a straightforward manner. Figure F-2 is an
example of a typical collector efficiency plot. Optical losses are shown as a constant
decrease in collector performance, while thermal losses increase as (Ti - Ta)/I increases.
The values of FRta and FRUL can be determined from this type of plot. FRta corresponds to
the intercept value where the collector efficiency curve crosses the vertical graph axis. FRta
is a dimensionless variable with a value between 0 and 1. FRUL is calculated by dividing
FRta by the intercept value on the horizontal axis (it is the negative slope of the plotted
line). FRUL has units of Btu per square foot per hour per degree F.
Figure F-2. Typical Collector Efficiency Curve
(e) Performance of Various Collector Types. Figure F-3 shows why
collector efficiency is not always a good indicator of overall collector performance. On
any given day, a solar collector can operate over a wide range of efficiencies as the
solar radiation, ambient temperature, and heat transfer fluid temperature change.
When insolation levels are low early in the day, the efficiency of the collector
approaches zero. As solar radiation levels increase, the collection efficiency increases
until it reaches some maximum level. It will then decrease as the solar insolation and
ambient temperature decrease at the end of the day. Because of the variable position
of the sun, collectors must be oriented so that they are exposed to an acceptable
amount of solar radiation throughout the year. Proper collector orientation and tilt
F-6




 Previous Page
Previous Page
