UFC 3-535-01
17 November 2005
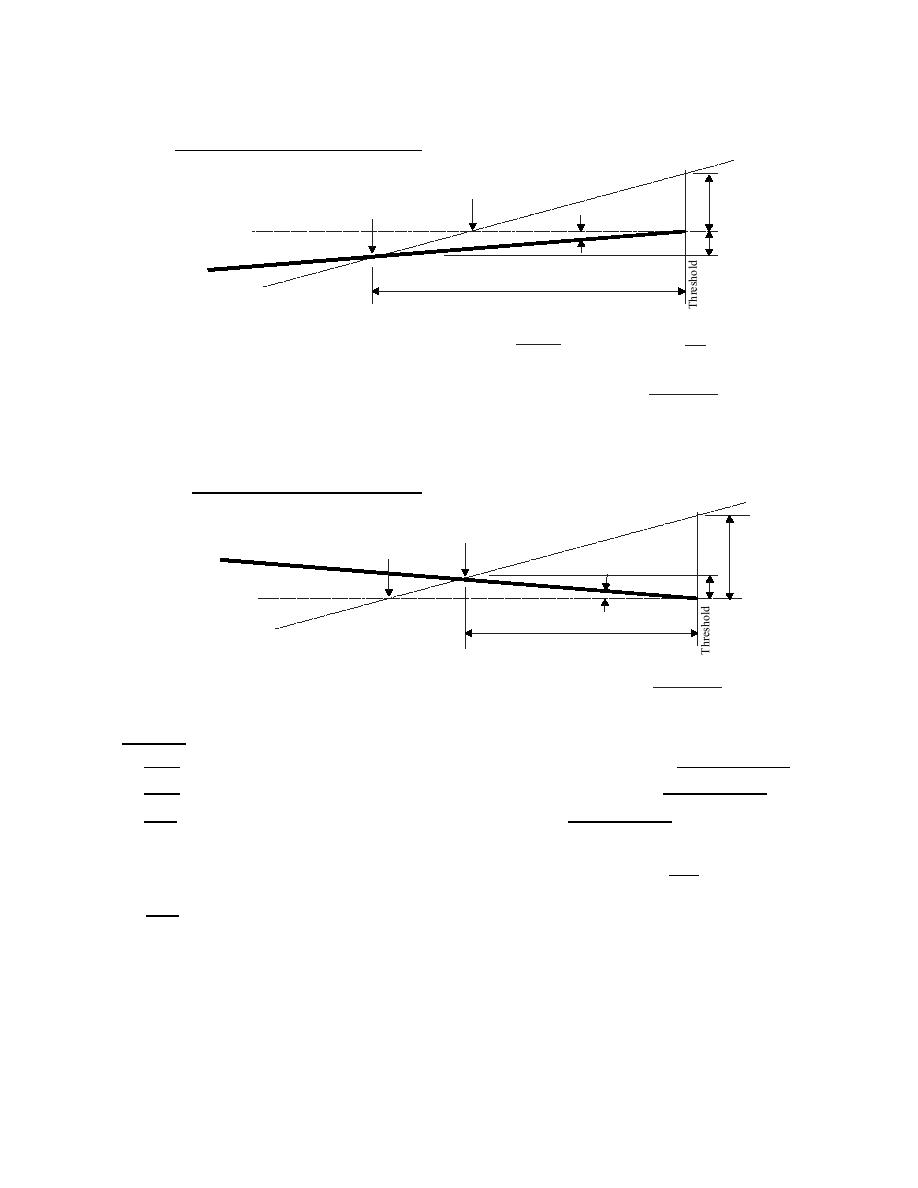
Figure 12-6. Siting PAPI without an ILS Glide Slope (1 of 2)
a. Case 1 - Runway with downward grade.
Ideal
ath, θ
RRP
p
Glide
TCH
RRP
Horizontal reference
Plane
h
RW slope, α
RW surface
d
Two relationships can be defined
TCH + h
h
tan α =
tan θ =
, and
which have two unknowns (d, h):
d
d
TCH
Substituting and solving the above, d is determined directly by:
d =
(tan θ - tan α)
b. Case 2 - Runway with upward grade.
ath, θ
RRP
p
Ideal
Glide
RRP
RW surface
TCH
RW slope, α
h
Horizontal reference
Plane
d
TCH
From the above relationships, d is determined directly by:
d =
(tan θ + tan α)
EXAMPLES (Assume the following: TCH = 15 meters (50 feet), θ = 3 degrees)
Case 1 (RW with 1% downward grade, α = 0.573 degrees) => d = 50/[tan 3 degrees - tan 0.573 degrees] = 360 meters (1,179 feet)
Case 2 (RW with 1% upward grade,(α = 0.573 degrees) => d = 50/[tan 3 degrees + tan 0.573 degrees] = 244 meters (801 feet)
Case 3 (RW is level - 0% grade, α and tan α are both 0) => d = 50/[tan 3 degrees] = 290 meters (954 feet)
[not illustrated]
While the slope should be constant through the first part of a runway, if the existing slope varies too much to directly apply Case 1, 2 or 3,
then a trial method illustrated by Case 4 can be used. In all cases, the location of the glide path intercept with the actual runway surface
(RRP) must be determined.
Case 4 - Runway grade varies too much to apply above methods => [See sheet 2 of 2]
173



 Previous Page
Previous Page
